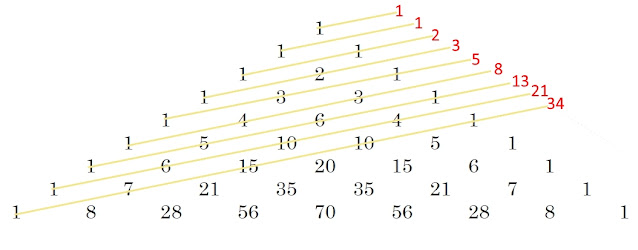
Blaise Pascal pioneered probability theory, but he is most famous for Pascal’s triangle, seen here: examine it to see how each row is generated from the one above, then draw up as many rows as possible on a single A4 sheet of paper. This example shows you how to tackle it.
Or if you prefer, create it on a spreadsheet and print it
out. Put the value 1 in cell K1, then type =A1+C1
in cell B2 and copy it all over the sheet. This puts a lot of unnecessary
zeroes in there: there are ways to get rid of them, but you need to find them.
Play with it!
Pascal’s triangle
has blocks of numbers that are all divisible by the same number. It is possible
to write a computer program to plot these into a diagram: try the numbers
divisible by three first, and then 5, and move up to larger numbers later.
By the way, if you
draw a slanting diagonal through the 1 at the left of the fifth row, then
through the leftmost 3 in the fourth row, and the 1 on the right of the third
row, the total of the numbers is 5. Now if you do the parallel diagonals above
and below and add the numbers on each diagonal, you will discover a wonderful
thing. Look at a few of them, and it will hit you: do those numbers ring a
bell?
Fibonacci has his numbers hiding in
Pascal’s triangle.
This is why this blog is called Playwiths!
To search this blog, use this link and then use the search box
Another way: use the index!






No comments:
Post a Comment