Sci: A speeding elephant

Schrödinger's Cheshire Elephant: this is a weird joke that will require some serious research.

The classification of animals and plants always involves a bit of opinion, and that can sometimes cause confusion. Aristotle did not exactly see that whales and porpoises were mammals, but he knew they were not like fish. Linnaeus, who invented our classification system, listed whales and porpoises as fish in the first ten editions of his book, Systema Naturae.

In the same way, 19th century scientists grouped elephants, rhinos and hippos as pachyderms. These were big, had thick grey skins, and came from Africa, but the grouping logic made as much sense as linking worms and wombats because they burrow, or butterflies and birds because they fly.

Still, the pachyderms were big and they had a formidable approach to threats: they charged them down. The pachyderms were big and heavy enough not to fear anybody or anything. They still are.

A rhinoceros will charge for short distances at 40 to 50 km/hr (25 to 30 mph), as timed by chargees in motor vehicles. Black rhinos (think of them as dark grey) have poor vision, and often break off, or run into a tree, but they are also very good at changing direction, which takes all the fun out of being charged. They tend to be aggressive to each other, and may keep up their charging speed for some time when chasing other black rhinos.

Hippos can certainly outrun a human on land, though estimates of their speed vary between 30 and 50 km/hr (18 to 30 mph). The hippos are vegetarians, but that does not seem to stop them attacking and killing humans: they have a reputation for killing more people in Africa than lions, though the Cape buffalo is also a contestant there. The good news: hippos can’t jump!

How to tell when an elephant is joking

Elephants walk at a sedate 7 km/hr or 4.5 mph, and they can keep that up for a considerable time. They have large territories, and need to keep moving, so as not to eat one area out, but when it comes to fighting their main enemy, humans, they accelerate to a higher pace.

African elephants will sometimes engage in what is called a mock charge, but at other times, they are deadly serious. In either case, the elephant will approach, people say, at some 50 km/hr (30 mph), and reversing at this speed can be risky, so safari drivers need to know the difference when 6 tons of elephants is heading your way.

In a mock charge, the elephant’s ears are standing out wide from the head and the trunk is curled. In a serious charge, the elephant has his ears back and trunk down, but there is more to the charge than that.

Researchers have discovered that elephants hear through their feet, sending out rumbles at 20 Hz, so low that humans can hardly hear them.

Sound travels through soils at around 3300 metres a second (that’s around 12,000 kph), almost ten times as fast as in air, and the low sound travels amazing distances: as much as 10 kilometres or six miles.

In nature, female elephants use the mock charge to chase off lions or hyenas, and the effect of moving the ears away from the head is to make her look even larger than she is. It is possible that the sounds emitted and transmitted across the African plains also vary, but that only other elephants can tell the difference.

And given that the speed of the elephant sounds through the ground exceed the escape velocity of our planet, it is just as well that elephants cannot charge as fast as their sounds can travel through the soil!

There is just one problem with the safari-driver claims, and that is the speed attributed to the elephant: John Hutchinson and his colleagues studied and videotaped large numbers of elephants, and found the highest speed observed was more like 25 km/hr or 15 mph. Older readers may recall the Four Minute Mile, which needed sustained running at 15 mph...

Butinterestingly, the elephants don’t run, even at top speed, not according to Olympic standards: they walk. The official definition of a walk is that at least one foot must be on the ground at any one time, and while elephants have been snapped with three feet off the ground, they have never been caught lifting all four at once.

To search this blog, use this link and then use the search box

Another way: use the index!

Sci: Speeding arrows

Estimation, unlike history, is a part of mathematics, and it is an important one, if you are relying on a calculator, where a slip of the finger can move the decimal point. Estimation is also useful for scientists when they don’t have complete and reliable data.

For example, until about 1600, most military firepower, aside from the odd cannon, used to batter walls from a distance, came from bows and arrows. In reality, up until the mid-1800s, it would have made more sense to keep on using archers, because a skilled bowman could fire more shots faster, doing greater harm at the end of their range, than a soldier could do, equipped with a rifle or a musket.

The key point is that an archer had to be skilled, and those who used longbows had to be strong. On the other hand, the skill and strength needed to fire a crossbow were low, like those needed to discharge a firearm. Crossbows fired fewer shots per minute than longbows, but they were more damaging than muskets.

The Aiming of the Shrew.

In October 1415, the small English army of King Henry V, some 6000 men, was faced at Agincourt with an army of 50,000 Frenchmen. The difference was not as great as you might think, because 5000 of the Englishmen were skilled archers. The French army was mainly composed of cavalry, and facing a rain of arrows, the French cavalry turned back into the French infantry, causing confusion that is bad for winning battles.

A good archer could fire off ten arrows a minute, each of them leaving the bow at 60 m/s (more than 200 km/h), and arriving a few seconds later, still carrying three quarters of that speed. All of these are estimates, of course, but we know that in 1590, Sir Roger Williams complained that only 10% of archers could do harm “12 or 14 score off”, which is at 240 to 280 yards, or 220 to 260 metres. Even at Waterloo in 1815, muskets had a range of less than 100 metres.

Much of the armour used at Agincourt was thin metal, perhaps 1 mm thick, and tests have shown that arrows would go through 1 mm steel. Some armour was up to 4 mm thick, and that would have withstood arrows, but not crossbow bolts.

The crossbow has the advantage that it can be loaded in advance, and used when necessary. More importantly, it fires a heavy bolt with real killing power, and no real training is needed to use one, because the operation is intuitive: point, steady the bow and shoot. After a ranging shot or two, most operators can be accurate enough to be dangerous.

The crossbow bolt would have been slower at first, but later ones are credited with ranges of a quarter of a mile (400 metres) and more. Allowing for air resistance, the bolts must have reached at least 75 m/s, close to 300 km/h. The rate of fire of the crossbow was comparable with that of a trained musket user, with less chance of a misfire, making the changeover to firearms (when it happened) a bit odd, because arrows, even crossbow ones, were still better. Perhaps the people in charge believed Zeno’s Paradox?

That same argument can also be applied with appropriate changes to an arrow approaching a target, but Zeno also said that if we divide the time into tiny enough segments, in each of them, the arrow is not moving. Either way, it will never reach the target. Remember the bumblebee!

To search this blog, use this link and then use the search box

Another way: use the index!

Sci: The art of estimation

 All tools can have surprising uses, and I once used a plumb bob to make my electricity supplier replace the power/light pole outside my house. I phoned them to report that the pole was in danger of falling and causing injury, but they ignored me. The second time I called, I told the person answering that the pole was 5.05º out of plumb, and that I was monitoring it, expecting the angle to increase.

The offending light pole and my high-tech equipment.

The operator was clearly suspicious of my claimed level of accuracy (as I would be, in the same position), and wanted to know how I measured it. “A plumb bob pinned, 1500 millimetres up the pole was 132 millimetres out at the base. That’s a sine of 0.088, and there’s my angle,” I said. The lesson: like tools, numbers also have surprising uses, and one of the best tricks is when you get to use numbers as a cattle prod—and common folk are alarmed by even simple science. The pole was replaced a week later, which was what I had estimated.

A very unlucky rabbit.

To a mathematician or physicist, the notion of an immortal rabbit is quite acceptable for calculation purposes. As a school student, my English teacher encouraged me to psychoanalyse Macbeth, even when I protested that Freud hadn’t been invented when Shakespeare was writing. Ever a historically-minded cuss, I argued that it would be more relevant to look at the political situation in London, with a Scot (James I) sitting on the throne. Exasperated, he urged the class to ignore me, to engage instead in the willing suspension of disbelief.

In the same way, a spherical horse or spherical cow can be a useful starting point to explore ideas, to get a first approximation that can be extended. That brings us to the claim about the bumblebee that was shown not to be able to fly: this is often trotted out as evidence that scientists are thick, but there is a little more to the story than that.

In 1934, a French entomologist called Antoine Magnan tried to apply an engineer’s equation to bumblebees, and showed how, according to that equation, designed for aircraft that did not flap their wings, the bee could not generate enough lift to take off.

There is a great deal of folklore wrapped around this “event” and who actually was involved, but it appears that the equation was worked out by André Saint-Lagué. While the incident is often dressed up as “a scientist proving that bumblebees can’t fly”, all that Magnan really showed was that the equation was inadequate to describe the flight of the bumblebee.

He had shown that you can’t apply that particular equation to bumblebees, rather than proving that spherical bumblebees can’t fly, even if real ones can, flapping their wings at 130 times a second, moving happily along at 3 metres/sec, 11 km/h. Like Zeno’s paradox, Magnan’s calculation merely showed that there was a faulty assumption in there somewhere. This minor paradox showed that the mathematical model was flawed.

Safely out of the English classroom and into the lab, we heard of the marvels that could be done with simple apparatus. The muzzle velocity of a bullet could be measured with just a block of wood, a piece of string, a protractor and a measuring tape.

Our physics teacher, as equally at home with fiction as our English teacher, explained how, in the days of gunpowder and muzzle-loading firearms, slight variations in the ingredients or their amounts and proportions, could make a lot of difference. In the 17^th and 18^th centuries, Britain and France were always at war, and better gunpowder could make all the difference between winning and losing. The very best saltpetre, an essential part of gunpowder, came from India.

The most obvious measure of powder quality was the speed at which a cannon ball or musket ball left the barrel of the gun, or in physics-speak, the muzzle velocity. The idea was quite simple. You suspended a large block of wood and fired a bullet at it from close range.

The bullet lodged in the block, and all the energy of the bullet was transferred to the block, which would swing like a pendulum. Then the researcher only had to measure the swing angle and calculate the height the block reached.

This gadget even has a name: it is the ballistic pendulum, and it was invented by Benjamin Robins in 1742. From the swing, or so we were told, it is an elementary calculation to estimate the energy and hence the velocity of the bullet. Unfortunately, this explanation ignores the 800-pound spherical horse that is rolling around the room. (OK, it could have been a spherical elephant, but that’s a different joke.)

Some of the energy would go into deforming the bullet and the wood, some would be wasted as friction, and to do any calculations, we would have to assume that the bullet stopped instantaneously (which is about as likely as a girder with negligible mass).

Of course, if you were simply trying to compare different grades of gunpowder, rather than measuring the muzzle velocities, the losses will be similar in each case, and they can be ignored. Whichever powder produces the biggest swing is the best, if everything else is kept constant, and in fairy physics (which is, you will recall, the name that engineers give to this sort of thinking), that always applies.

Robins’ ballistic pendulum would have shown that Indian saltpetre made the best gunpowder. He died in India in 1751, supervising the construction of forts, and a few years later, the British drove the French out of India, getting all that excellent saltpetre for their own use. (History is one of the Arts, but chemistry has to be understood as well.)

And you need to keep an open mind. When you enquire about fast animals, more often than not, you will read that the fastest animal of all is the deer botfly. This is credited with an amazing 1287 km/hr, though if you convert this to miles per hour, that comes out as a round 800 mph, a figure that smells a little bit of fudged science—and rightly so, because round numbers are always suspicious.

A 1927 article in the Journal of the New York Entomological Society, written by an entomologist called Charles Henry Tyler Townsend reported a speed like that. Townsend said these flies passed in a blur, and so must have been travelling very fast. On that ‘scientific’ basis and no other, he credited the flies with a nice round 400 yards per second.

In 1938, when Irving Langmuir, a Nobel laureate in chemistry tested the assumptions. He found that the air pressure on the fly at that speed would be more than half an atmosphere, enough to crush it. The energy needed to maintain the flight would be 370 watts, half a horsepower. Aside from anything else, the fly would use up its own weight in fuel every second.

Langmuir had been hit by these flies, and while it hurt, a fly of that weight, going at 1300 km/hr would have left a significant hole in him, rather like that of a soft bullet, and the fly would have been mashed inside the wound. Instead, the fly bounced off. He used solder to make a pellet, the size of a fly, 1 cm long and 0.5 cm wide, and tied it to a string.

He whirled the pellet around his head. Knowing the length of the string and how many circuits it made each second, he calculated the speed, and found that at 13 mph, it was a blur. At 26 mph, it was barely visible; at 43 mph, an observer could not tell which way it was going; and at 64 mph, it was invisible. He said Townsend’s blur came from a fly travelling at 25 mph (40 km/hr).

Langmuir’s results were published in Science and reported in Time magazine, but legends are tough things, even when they are debunked by Nobel Prize winners. So even today, the same old values keep emerging from the woodwork.

Post script 1: catching crooks with numbers

When one is engaged in fraud investigation, one fertile method is to do some rough estimating, because these will often show up fraud. If an operation averages eight sick days per worker each year, you can make certain assumptions. If after allowing for seasonal colds and the like, the averages or the frequencies don’t fit the estimates, a closer look is recommended.

Post script 2: a floating cork

I was once asked (never mind why) to calculate the mass of a cork ball, two metres in diameter. Getting the volume is easy: ⁴/₃ x πr³ or 4.189 cubic metres, but how much does a cubic metre of cork weigh? There are two ways to find out: one is to look it up, the other is to estimate it, by looking at a cork in water.

Estimating the density of cork.

I decided that 20% of the cork in the photo above was submerged, giving a density of 0.2, while the reference books give a value of 0.24. My estimated mass was 838 kg, while the official answer would be just over 1000 kg. As they say. near enough for government work, and this was, as it happens, government work.

Whatever: under each answer, a 2-metre cork ball was a bad idea in a children’s playground! Oops, I gave the why away, but my calculations saved somebody else’s job, and perhaps a life or two.

Post script 3: Round numbers

There is a legend that the surveyors who measured the height of Mount Everest found that the numbers they had gave a value of exactly 29,000 feet, but they decided that nobody would accept that, so they gave the value as 29,002 feet (8,839.8 m), fearing that the calculated value of 8,839.2 m would be dismissed as a rounded estimate. This remains a conjecture that most scientists would like to be true.

To search this blog, use this link and then use the search box

Another way: use the index!

Maths: Pascal’s marvellous triangle

Blaise Pascal pioneered probability theory, but he is most famous for Pascal’s triangle, seen here: examine it to see how each row is generated from the one above, then draw up as many rows as possible on a single A4 sheet of paper. This example shows you how to tackle it.

Pascal’s triangle.

Or if you prefer, create it on a spreadsheet and print it out. Put the value 1 in cell K1, then type =A1+C1 in cell B2 and copy it all over the sheet. This puts a lot of unnecessary zeroes in there: there are ways to get rid of them, but you need to find them. Play with it!

Pascal’s triangle has blocks of numbers that are all divisible by the same number. It is possible to write a computer program to plot these into a diagram: try the numbers divisible by three first, and then 5, and move up to larger numbers later.

By the way, if you draw a slanting diagonal through the 1 at the left of the fifth row, then through the leftmost 3 in the fourth row, and the 1 on the right of the third row, the total of the numbers is 5. Now if you do the parallel diagonals above and below and add the numbers on each diagonal, you will discover a wonderful thing. Look at a few of them, and it will hit you: do those numbers ring a bell?

Fibonacci has his numbers hiding in Pascal’s triangle.

This is why this blog is called Playwiths!

To search this blog, use this link and then use the search box

Another way: use the index!

Maths: Can we trust statistics?

 

Show this engraving to a nearby tame adult, and he or she will probably guess know that this is “The Lady with the Lamp”, Florence Nightingale, who turned nursing into a profession. Tame adults are unlikely to know that the engraving was by James-Charles Armytage, and they are even more unlikely to know what Florence Nightingale did for statistics, using them to argue for reforms in nursing.

To rally public support for nursing reforms, she wrote a pamphlet called Mortality in the British Army, and this was the first use of pictorial charts to present data. She invented all those diagrams in the financial pages, with wheat bags, or oil barrels or human figures lined up like so many paper dolls. She hammered away again in 1858 in her Report on the Crimea:

It is not denied that a large part of the British force perished from causes not the unavoidable or necessary results of war...(10,053 men, or sixty percent per annum, perished in seven months, from disease alone, upon an average strength of 28,939. This mortality exceeds that of the Great Plague)...The question arises, must what has here occurred occur again?

In 1858, Nightingale was elected to the newly formed Statistical Society and turned her attention to hospital statistics on disease and mortality. Now read on…

This entry began as two radio talks delivered on the ABC, more than thirty years ago. My friend Peter Chubb asked me later if I had addressed these issues in a book that was in progrtess, and I said that I hadn’t, but that I had provided a link to the text of the talk. Two nights later, I decided to add it to then book, the next night, I rewrote it. Here is a tweaked version.

There is enough information here to let readers try this one-paragraph exercise in Evil Statistics out for themselves.

Boris, Don and Scotty went fishing, and caught ten fish. Four weighed 1 kg, two were 2 kg, two were three kg, one was 6 kg, and one was 10 kg. They reported that the average was 1 kg, 2 kg and 3 kg, and all were telling a sort of truth. Boris reported the mode, the most common mass, Don reported the median, the masses of the middle two fish, Scotty reported the mean, adding all the masses and dividing by ten. Each value was true, each was different.

It all sounds a bit like “Lies, damned lies, and statistics”, but who first said that? The popular myth is that it was Mr. Disraeli, the well-known politician, but many quite reputable and reliable reference books blame author Mark Twain.

It turns out that it was first published by Twain all right, but Twain attributed the line to Disraeli, and you won't find the story in any earlier publication than Twain's autobiography. In short, Mark Twain made the whole thing up! Disraeli never spoke those words: Twain invented them all, but he wanted the joke to have a greater force, and so gave the credit to an English politician.

Twain wasn't only well-known for his admiration of a good “Stretcher” (of the truth, that is), he even lied when he was talking about lies, and his name wasn't even Mark Twain, but Samuel Clemens! Now would you buy a used statistic from this man?

Last century, when Disraeli is supposed to have made the remark, statistics were just numbers about the State. The state of the State, all summed up in a few simple numbers, you might say.

Now governments being what they are, or were, there was more than a slight tendency in the nineteenth century to twist things just a little, to bend the figures a bit, to bump up the birth rate, or smooth out the death rate, to fudge here, to massage there, to adjust for the number you first thought of, to add a small conjecture or maybe to slip in the odd hypothetical inference.

It was all too easy to tell a few small extravagances about one's armaments capacity, or to spread the occasional minor numerical inexactitude about whatever it was rival nations wanted to know about, and people did just that. Even today, when somebody speaks of average income, if you don’t smell fish, at least remember them, and ask if that’s the mean, the median or the mode.

When I was young, I smoked cigarettes, but the cost and the health risks convinced me, so I stopped, back in 1971. Smokers think we reformed smokers are tiresome people who keep on at them, trying to get them to stop as well.

The non-smokers say those who still puff smoke are the tiresome people, who can't see the carcinoma for the smoke clouds, who deny any possibility of any link between smoking and anything. Like the tobacco pushers, the smokers dismiss the figures contemptuously as “only statistics”. The really tiresome smoker will even say a few unkind things about the statisticians who are behind the figures. Or about the statisticians who lie behind the figures.

By the end of the 19th century, statistics were no longer the mere playthings of statesmen, they were way to clump large groups of related facts into convenient chunks. If you can see how the statistics were arrived at, perhaps you can trust them.

At one stage in my career, I led a gang of people who gathered statistics and messed about with numbers, but we preferred to be called ‘number-crunchers’. People say a statistician is “somebody who's rather good around figures, but who lacks the personality to be an accountant”.

They speak of the statistician who drowned in a lake with an average depth of 15 cm. We are told that a statistician collects data and draws confusions, or draws mathematically precise lines from an unwarranted assumption to a foregone conclusion. They say “X uses statistics much as a drunkard uses a lamp-post: rather more for support than for illumination”.

Crusty old conservatives give us a bad name, pointing out that tests reveal that half our nation's school leavers to be below average, which is true, but it is equally true that the vast majority of Australians have more than the average number of legs. Think about it: all you need is one Australian amputee!

If somebody does a Little Jack Horner with a pie that's absolutely bristling with statistical items and they produce just one statistical plum, I won't be impressed at all: the plum's rather more likely to be a lemon, anyhow. The statistics have to be plausible and significant. Later, I will show you a statistical link between podiatrists and public telephones: this is obviously nonsense, and we should ignore it. There is no logical reason for either to influence the other.

Still, unless there is a plausible reason why X might cause Y, it's all very interesting, and I'll keep a look-out, just in case a plausible reason pops up later, but I won't rush to any conclusion. Not just yet, I won't.

First, I will check on the likelihood of a chance link, something we call statistical significance. After all, if somebody claims to be able to tell butter from margarine, you wouldn't be too convinced by a single successful demonstration, would you? Well, perhaps you might be convinced: certain advertising agencies think so, anyway.

If you tossed a coin five times, you wouldn't think it meant much if you got three heads and two tails, unless you were using a double-headed coin, maybe. If somebody guessed right three, or even four, times out of five, on a fifty-fifty bet, you might still want more proof.

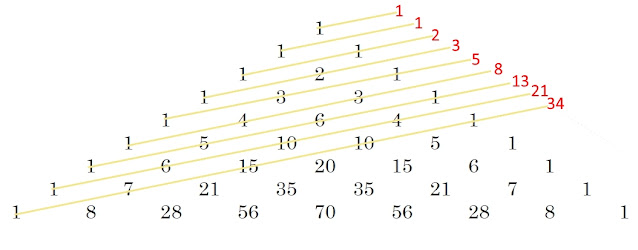
You should, you know, for there's a fair probability it was still just a fluke, a higher probability than most people think. There's about one chance in six of correctly guessing four out of five fifty-fifty events. Here is a table showing the probabilities of getting zero to five correct from five tosses:

zero right	one right	two right	three right	four right	five right
1/32	5/32	10/32	10/32	5/32	1/32

The clever reader may notice a resemblance to Pascal’s triangle here! Now back to the butter/margarine study. Getting one right out of one is a fifty-fifty chance, while getting two right out of two is a twenty five per cent chance, still a bit too easy, maybe. So you ought to say “No, that's still not enough. I want to see you do it again!”.

Statistical tests work in much the same way. They keep on asking for more proof until there's less than one chance in twenty of any result being just a chance fluctuation. The thing to remember is this: if you toss a coin often enough, sooner or later you'll get a run of five of a kind.

As a group, scientists have agreed to be impressed by anything rarer than a one in twenty chance, quite impressed by something better than one in a hundred, and generally they're over the moon about anything which gets up to the one in a thousand level. That's really strong medicine when you get something that significant.

Did you spot the wool being pulled down over your eyes, did you notice how the speed of the word deceives the eye, the ear, the brain and various other senses? Did you feel the deceptive stiletto, slipping between your ribs? We test statistics to see how “significant” they are, and now, hey presto, I'm asserting that they really are significant. A bit of semantic jiggery-pokery, in fact.

That's almost as bad as the skullduggery people get up to when they're bad-mouthing statistics. Even though something may be statistically significant, that's a long way away from the thing really being scientifically significant, or significant as a cause, or significant as anything else, for that matter.

Statistics make good servants but bad masters. We need to keep them in their places, but we oughtn't to refuse to use statistics, for they can serve us well. Now you are ready to object when I assert that all the podiatrists in New South Wales seem to be turning into public telephone boxes in South Australia, and it all began with Florence Nightingale. Most people think of her as the founder of modern nursing, but as part of that she created ways to use statistics to pinpoint facts.

After her name was made famous, directing nursing in the Crimean war, she returned to London in 1857, and started to look at statistics, and the way they were used. She wrote a pamphlet called “Mortality in the British Army”, and the very next year, she was elected to the newly formed Statistical Society.

She looked at deaths in hospitals, and demanded that they keep their figures in the same way. The Statistical Congress of 1860 had, as its principal topic, her scheme for uniform hospital statistics. It isn’t enough to say Hospital X loses more patients than Hospital Y does, so therefore Hospital X is doing the wrong thing.

We need to look at the patients at the two hospitals, and make allowances for other possible causes. We have to study the things, the variables, which change together. Statistics, remember, are convenient ways of wrapping a large amount of information up into a small volume. A sort of short-hand condensation of an unwieldy mess of bits and pieces.

And one of the handiest of these short-hand describers is the correlation coefficient, a measure of how two variables change at the same time, the one with the other. Now here I'll have to get technical for a moment. You can calculate a correlation coefficient for any two variables, things like number of cigarettes smoked, and probability of getting cancer.

The correlation coefficient is a simple number which can suggest how closely related two sets of measurements really are. It works like this: if the variables match perfectly, rising and falling in perfect step, the correlation coefficient comes in with a value of one. But if there's a perfect mismatch, where the more you smoke, the smaller your chance of surviving, then you get a value of minus one.

With no match at all, no relationship, you get a value somewhere around zero. But consider this: if you have a whole lot of golf balls bouncing around together on a concrete floor, quite randomly, some of them will move together, just by chance.

There’s no cause, nothing in it at all, just a chance matching up. And random variables can match up in the same way, just by chance. And sometimes, that matching-up may have no meaning at all. This is why we have tests of significance. We calculate the probability of getting a given correlation by chance, and we only accept the fairly improbable values, the ones that are unlikely to be caused by mere chance.

We aren’t on safe ground yet, because all sorts of wildly improbable things do happen by chance. Winning the lottery is improbable, though the lotteries people won't like me saying that. But though it's highly improbable, it happens every day, to somebody. With enough tries, even the most improbable things happen.

So here's why you should look around for some plausible link between the variables, some reason why one of the variables might cause the other. But even then, the lack of a link proves very little either way. There may be an independent linking variable.

Suppose smoking was a habit which most beer drinkers had, suppose most beer drinkers ate beer nuts, and just suppose that some beer nuts were infected with a fungus which produces aflatoxins that cause slow cancers which can, some years later, cause secondary lung cancers.

In this case, we'd get a correlation between smoking and lung cancer which still didn't mean smoking actually caused lung cancer. And that's the sort of grim hope which keeps those drug pushers, the tobacco czars going, anyhow. It also keeps the smokers puffing away at their cancer sticks.

It shouldn't, of course, for people have thrown huge stacks of variables into computers before this. The only answer which keeps coming out is a direct and incontrovertible link between smoking and cancer. The logic is there, when you consider the cigarette smoke, and how the amount of smoking correlates with the incidence of cancer. It's an open and shut case.

I'm convinced, and I hope you are too. Still, just to tantalise the smokers, I'd like to tell you about some of the improbable things I got out of the computer in the 1980s. These aren't really what you might call damned lies, and they are only marginally describable as statistics, but they show you what can happen if you let the computer out for a run without a tight lead.

Now anybody who's been around statistics for any time at all knows the folk-lore of the trade, the old faithful standbys, like the price of rum in Havana being highly correlated with the salaries of Presbyterian ministers in Massachusetts, and the Dutch (or sometimes it's Danish) family size which correlates very well with the number of storks' nests on the roof.

More kids in the house, more storks on the roof. Funny, isn't it? Not really. We just haven't sorted through all of the factors yet. The Presbyterian rum example is the result of correlating two variables which have increased with inflation over many years.

You could probably do the same with the cost of meat and the average salary of a vegetarian, but that wouldn't prove anything much either. In the case of the storks on the roof, large families have larger houses, and larger houses in cold climates usually have more chimneys, and chimneys are what storks nest on. So naturally enough, larger families have more storks on the roof. With this information, the observed effect is easy to explain, isn't it?

There are others, though, where the explanation is less easy. Did you know, for example, that Hungarian coal gas production correlates very highly with Albanian phosphate usage? Or that South African paperboard production matches the value of Chilean exports, almost exactly?

Or did you know the number of iron ingots shipped annually from Pennsylvania to California between 1900 and 1970 correlates almost perfectly with the number of registered prostitutes in Buenos Aires in the same period? No, I thought you mightn't.

These examples are probably just a few more cases of two items with similar natural growth, linked in some way to the world economy, or else they must be simple coincidences. There are some cases, though, where, no matter how you try to explain it, there doesn't seem to be any conceivable causal link. Not a direct one, anyhow.

There might be indirect causes linking two things, like my hypothetical beer nuts. These cases are worth exploring, if only as sources of ideas for further investigation, or as cures for insomnia. It beats the hell out of calculating the cube root of 17 to three decimal places in the wee small hours, my own favourite go-to-sleep trick.

Now let's see if I can frighten you off listening to the radio, that insomniac's stand-by. Many years ago, in a now-forgotten source, I read that there was a very high correlation between the number of wireless receiver licences in Britain, and the number of admissions to British mental institutions.

At the time, I noted this with a wan smile, and turned to the next taxing calculation exercise, for in those far-off days, all correlation coefficients had to be laboriously hand-calculated. It really was a long time ago when I read about this effect.

It struck me, just recently (that was 40 years ago!), that radio stations pump a lot of energy into the atmosphere. In America, the average five-year-old lives in a house which, over the child's life to the age of five, has received enough radio energy to lift the family car a kilometre into the air. That's a lot of energy.

Suppose, just suppose, that all this radiation caused some kind of brain damage in some people. Not all of them necessarily, just a susceptible few. Then, as you get more licences for wireless receivers in Britain, so the BBC builds more transmitters and more powerful transmitters, and more people will be affected. And so it is my sad duty to ask you all: are the electronic media really out to rot your brains? Will cable TV save us all?

Presented in this form, it's a contrived and, I hope, unconvincing argument. Aside from anything else, any physicist can tell you that the radiation used for radio transmission is the wrong wave-length and lacks the energy needed to change any cells. My purpose in citing these examples is to show you how statistics can be misused to spread alarm and despondency. But why bother?

Well, just a few years ago, problems like this were rare. As I mentioned, calculating just one correlation coefficient was hard yakka in the bad old days. Calculating the several hundred correlation coefficients you would need to get one really improbable lulu was virtually impossible, so fear and alarm seldom arose.

That was before the day of the personal computer and the hand calculator. Now you can churn out the correlation coefficients faster than you can cram the figures in, with absolutely no cerebral process being involved.

As never before, we need to be warned to approach statistics with, not a grain, but a shovelful, of salt. The statistic which can be generated without cerebration is likely also to be considered without cerebration.

And that brings me, slowly but inexorably to the strange matter of the podiatrists, the public telephones, and the births.

Seated one night at the keyboard, I was weary and ill at ease. I had lost one of those essential connectors which link the parts of one's computer. Then I found the lost cord, connected up my computer, and fed it a huge dose of random data.

I found twenty ridiculously and obviously unrelated things, so there were one hundred and ninety correlation coefficients to sift through. That seemed about right for what I was trying to do. which was to show that figures may prove nothing at all.

When I was done, I switched on the printer, and sat back to wait for the computer to churn out the results of its labours. The first few lines of print-out gave me no comfort, then I got a good one, then nothing again, then a real beauty, and so it went: here are my cunningly selected results.

Remember: I have simply used, for honest reasons, the methods of the crooks and con-men.

	Tasmanian birth rate	SA public phones	NSW podiatrist registrations
Tasmanian birth rate	1	+0.94	-0.96
SA public phones	+0.94	1	-0.98
NSW podiatrist registrations	-0.96	-0.98	1

Well of course the podiatrists and phones part is easy. Quite clearly, New South Wales podiatrists are moving to South Australia and metamorphosing into public phone boxes. Or maybe they're going to Tasmania to have their babies, or maybe Tasmanians can only fall pregnant in South Australian public phone booths.

Or maybe codswallop grows in computers which are treated unkindly. Figures can't lie, but liars can figure. I would trust statistics any day, so long as I can find out where they came from, and I would even trust statisticians, so long as I knew that they knew their own limitations. Most of the professional ones do know their limitations: it's the amateurs who are dangerous.

I'd even use statistics to choose the safest hospital to go to, if I had to go. But I'd still rather not go to hospital in the first place.

After all, statistics show clearly that more people die in the average hospital than in the average home.

A note about statistics

At one stage in my working life, allegedly professional colleagues would come to see me for help with “crunching their numbers”, but a statistic is a number that gives you a quick summary. Quite often they only had the summary numbers, and the original data had been tossed out. Whatever you do, never, ever, ever throw away any of the data, until well after all of the analysis and discussion is finished!

To search this blog, use this link and then use the search box

Another way: use the index!

Arts: advanced verse writing

 Verse using sayings

I like constructing versicles that have a well-known line sneaking in at the end. The trick is to begin with the final line.

The Dark Knight
The knight rode up, in squeaking armour,
Fury writ upon his brow
And strange to say, he rode a lama—
A thief had nicked his favourite cow.

A knight whose thing was riding cattle?
I hear you ask, in rising fear.
Why yes, he did, even in battle—
His horse he’d sold to pay for beer.

His helm was sable, like his rage
And black was all the gear he wore
Save on his arm an off-white gage
But black was the stubble on his jaw.

He slapped his shield upon the bar,
His shield with the motto “Ebon semper”
He made it clear, both near and far
He had a really nasty temper.

He kicked the spittoon over twice
And gave the crowd a dreadful fright
And then they saw, as in a trice:
It was a dark and stormy knight.

Kids and lambs
I recall, one winter’s day,
Our mothers led us out to play
And we took off our hats and coats
And romped among the sheep and goats.

Our mothers had gone out to paint
The scene, but one fell in a faint.
The other mothers brought her round,
And that was when we children found

She thought it made us all look cheap
To frolic with the goats and sheep.
She wanted us, midst rocks and greenery
To form part of the painters’ scenery.

When faced with such artistic needs,
Obedient youngsters mould their deeds.
We children gave our solemn word
That we’d be scene but never herd.

This last one comes from a question I was asked once in Luang Prabang in Laos.

My frypan is a handy size
For cooking food and swatting flies
So if you want things cooked in fat
I’ll say “Would you like flies with that?

To write amusing verse, you have to be an opportunist! Then again, a lot of science began with somebody seeing something odd, and grabbing the opportunity.

Verse about the seasons

There are very few simple verses about the seasons as we encounter them in Australia. I am working on a set myself, at the moment, so I know it can be done. I am not about to reveal those here, but I am prepared to challenge you to do better, without seeing what I have done.

Work on a plan of 4 to 12 lines in verses of 4 or 6 lines, using rhyming schemes like abab, cdcd etc., or maybe aabccb etc. Pay VERY careful attention to where the stresses come, and see how much scientific background and Australian natural history you can slip in.

The main thing to recall is that finding rhymes for the seasons can be extremely hard, so work on finding other words that are easier to rhyme, something like:

The trouble with summer: it’s hot;
The trouble with winter: it’s not.

OK, not one of my best, but you get the idea. Pay some attention to the punctuation—you would be amazed how much information you can give to the reader with the right punctuation marks.

Master Class: Piet Hein’s grooks

Elsewhere, you have met the soma cube and a superellipse that were invented by Piet Hein (1905 – 1996), a Danish inventor, scientist, mathematician, philosopher, designer, author, and poet.

Hein specialised in short verses that made people think, like these:

ATOMYRIADES
Nature, it seems, is the popular name
for milliards and milliards and milliards
of particles playing their infinite game
of billiards and billiards and billiards.

OMNISCIENCE
Knowing what
thou knowest not
is in a sense
omniscience.

Look him up, and then try your hand at a few grooks of your own.

To search this blog, use this link and then use the search box

Another way: use the index!

Arts: Writing verse on STEAM topics

Who says there’s no room for verse or whimsy in science? Wise people say you can’t teach poetry, but most practising writers know you can teach verse-making. As one of Australia’s better 20^th century poets taught me, if you want to rhyme platitude and attitude, always use the more common word (attitude) second. Do it the other way, and the rhyme seems forced. This chapter is all about creating rhymes that appear unforced.

One of the problems with being an adult is that you have to attend meetings. In these, you have to pretend to be interested, and that means apparently taking notes. If your hand-writing is as bad as mine, nobody can tell that you are writing, especially if you are writing verse, and don't insert line breaks.

Almost any topic will do, and they can be serious or comic. I will start with some efforts from masters. Haldane (next) is a particular favourite of mine. He let his verse out for a run quite often.

Miss Robinson and R. McCance
Have made a notable advance
On dealing with tyrosinase,
And the queer laws which it obeys.
Aided by Anderson and others
Our saccharologist Carruthers
Attacked the problem of rotation
Of glucose during activation.
—J.B.S. Haldane, Report to the Secretary of the Sir William Dunn Institute for the Year 1924-25.

Cuspidors made out of platinum
Would buckle and bend if you sat in 'em.
  You can make them of rhodium
  But never of sodium
Because then they'd explode if you spat in 'em.
— attributed to Sir John Cornforth, Australian-born chemistry Nobel laureate.

Science

There was a young lady named Bright,
Who travelled much faster than light.
  She started one day
  In a relative way,
And returned on the previous night.
— Anon. and trad.

I think that I shall never see
A poem lovely as a tree
— Joyce Kilmer (1886-1918) Trees

Great fleas have little fleas upon their backs to bite 'em,
And little fleas have lesser fleas and so ad infinitum.
And the great fleas themselves, in turn, have greater fleas to go on;
While those again have greater still, and greater still, and so on.
— Augustus de Morgan (1806 - 1871)

Water is H2O, hydrogen two parts, oxygen one,
but there is also a third thing, that makes it water
and nobody knows what that is.
— D. H. Lawrence (1885 - 1930), Pansies, 'The Third Thing'.

Twinkle, twinkle little star,
I don't wonder what you are,
For by spectroscopic ken
I know that you are hydrogen.
— Anon

“I quite realised,” said Columbus,
“That the earth was not a rhombus,
But I am a little annoyed,
To find it an oblated spheroid.”
— Edmund Clerihew Bentley (1875 – 1956) (see Clerihews, below)

Technology

We tell these tales, which are strictly true,
Just by way of convincing you
How very little, since things was made,
Anything alters in anyone's trade.
— Rudyard Kipling (1865 - 1936), A Truthful Song.

I heard him then, for I had just
  Completed my design
To keep the Menai bridge from rust
  By boiling it in wine.
— Lewis Carroll (Charles Lutwidge Dodgson) (1932 - 1898), Through the Looking-Glass, chapter VIII.

Gold is for the mistress — silver for the maid —
Copper for the craftsman cunning at his trade.
'Good!' said the Baron, sitting in his hall,
'But Iron — Cold Iron — is master of them all.'
— Rudyard Kipling (1865 - 1936) Cold Iron.

Engineering

They shut the path through the woods
Seventy years ago.
Weather and rain have undone it again,
And now you would never know
There was once a path through the woods.
— Rudyard Kipling (1865 - 1936), The Way through the Woods.

Arts

There once was a brainy baboon,
Who always breathed down a bassoon,
         For he said, 'It appears
         That in billions of years
I shall certainly hit on a tune'.
— Sir Arthur Eddington (1882 - 1944), New Pathways in Science.

Mathematics

There was a young man from Trinity
Who solved the square root of infinity.
  While counting the digits,
  He was seized by the fidgets,
Dropped science, and took up divinity.
— Anon. 

The platypus egg
Has a single leg
On which it stands
To save its hands
— Duncan Bain (1944 - ), 'The platypus egg' in Self-reverenced Sentiences (n.p.). (used by permission)

Medicine

He prayeth best who loveth best
All things great and small.
The Streptococcus is the test
I love him least of all.
—Hilaire Belloc (but was he the author? As it happens, I wrote about this in my other blog. )

Clerihews

Clerihews are a simple verse form invented by Edmund Bentley (whose middle name was Clerihew). These are amusing “potted biographies” of people. They do not need to have a rhythm (a metre, if you are pedantic), but they must have a rhyme, and they must say something about the person involved who has to be historical. Here is an example:

George the Third
Ought never to have occurred.
One can only wonder
At so grotesque a blunder.

Limericks must have a perfect metre and astounding rhymes, but clerihews don’t have to scan. The aim is to be historically correct in an odd sort of way, and to get a dreadful, weird rhyme. Here are two more examples:

Sir Christopher Wren
Said: “I am going to dine with some men.
If anybody calls,
Say I’m designing St Paul’s.”

Sir Humphry Davy
Abominated gravy.
He lived in the odium
Of having discovered sodium

Now it is time for you to try your hand. Here are some names to get started on. Most should be accessible to most people, and some are drawn from areas other than science, so feel free to pick and choose. These people will all be found, somewhere on the internet.

 

Julius Caesar	Mary Anning	Louis Pasteur	Stephen Hawking
Dame Nellie Melba	Sir Isaac Newton	Marie Curie	Enrico Fermi
Catherine the Great	Pablo Picasso	Nebuchadnezzar	Agatha Christie
Annie Jump Cannon	Burke and Wills	Kiri Te Kanawa	Jakob Bernoulli

 

Here’s just one of my attempts:

Burke and Wills
Were paying their bills,
When somebody said
Why bother? You’re dead!

Remember that you will need to investigate each of these people before you write your clerihew, and find out what they did, or do.

Just look at the examples, then do some researching before you start scribbling. Historical accuracy is never important, but historical relevance always matters. Try these starters:

Louis Pasteur                             Marie Curie
Was a him, not a her,                  Got into a fury

Jakob Bernoulli                          Pablo Picasso
Was often unruly                        Sang a rumbling basso

Florence Nightingale                   Ernest Hemingway
Always read her nightly mail        Went out the lemming way

Charles Babbage                         Alexander Graham Bell,
Hated cabbage                           Completely lost his sense of smell

Mary Anning                              Agatha Christie
Took up gold panning                 Had eyes that went misty

Samuel Morse                            Edward John Eyre
Was a vegan of course                Started losing his hair

To search this blog, use this link and then use the search box

Another way: use the index!